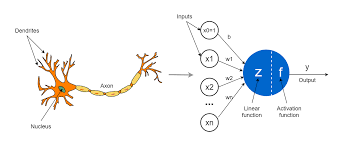
引言:数据无处不在
想象一个你熟悉的日常活动,它涉及大量数据:几点做什么,做了多久,做得如何,从1到10给自己打几分。而你的基本信息——身高165cm,体重50kg,年龄18岁——也都是数据的一种形式。
一个有趣的问题浮现:既然所有信息都可以表达为数据,那么有没有一种模型,能够计算出你在某一时刻的状态——你正在做什么、心情如何、身处何地?
理论上,这种可能性是存在的。只要人类的语言和认知足够发达,一切信息都是数据。既然是数据,就有模式(pattern),就可以计算。于是我们可以依赖一个模型:输入数据,经过计算,输出数据。
理想与现实的碰撞
那么这个模型怎么实现呢?
在理想世界中,水晶球可能是这个模型。我希望有一天走在路上能捡到个水晶球,通过它看到未来和过去的信息。机器猫的口袋也可能是这个模型——想要什么,都能在口袋里取出一个对应功能的道具,完全不用考虑存在的逻辑,就是凭空产生,并且满足了我们上面谈到的”一个输入、一次计算、一个输出”。
但这只存在于想象中,无法在现实中实现。
现实世界的第一条规则:遵守规则。你不能凭空创造一个东西,而是需要根据理论、材料、工程可行性,进行逻辑创造。也就是说,我们对这个世界理解多少,我们就能创造多少。
记住这个规则很重要。有了这个准则,你可以用来评价一个技术的发展是泡沫、是炒作hype,还是实打实有理有据、有潜力的。
以机器人研发为例,最初人类有了”造一个像自己一样的智能人”的概念,然后基于工程、电子、传感器、光学、声学等理论,才一步步让机器人能走、能跳、能看、能说。
机器人的视觉之所以能实现,是因为我们已经知道人眼是怎么成像的:物体反射光线传入眼睛,眼睛就是一套光学系统,光线进入瞳孔、通过晶状体、投射在视网膜上;接着通过视觉神经传入大脑特定区域进行构建、感知和处理,最终”看到”。那么机器成像也得遵循这个道理:首先得制造类似人眼结构的相机进行成像,接着是理解图像,识别出猫是猫,狗是狗。
总之,一项新技术的产生,在概念诞生之后,得有对现实世界真实存在的实体的理解,也就是理论,接着是材料,然后是工程实践的可行性。
深度学习:现实中的模型
回到一开始我们设想的这个模型,目前能实现这个功能的,最简单的就是深度学习网络。
什么是深度学习?就是一个系统或模型,学习了大量数据的形状和特征,具有多层计算结构,可以接受数据的输入,产生数据的输出。
理解概念的第一法则:从最简单的模型开始
谈到理解一个概念,第一法则是:先理解最简单的模型。
- 当我们谈论模型,可以直接简化为一个函数
- 一个输入
- 一个输出
比如常量函数 y = 1,接受 x = 1,输出1。这也是一个模型,但这个模型没什么实际意义,因为现实世界是变化的,这个模型没有适用的地方。
我们可以进一步复杂点,来一个线性函数:y = wx + b。这个模型是变化的,比常量函数有用了一点。假如 w = w₀,b = b₀,那么 y = w₀x + b₀ 这个函数可以用来描述我在某年的年龄。这个模型可不得了,我可以知道我哪年的年龄是多少,这可有用了。
==这就是我喜欢的逻辑,有了假设,才能进一步讨论==。
寻找正确的w₀
但事实上,我并不知道 w₀、b₀ 具体是多少,但我知道什么是对的:我2025年刚满18岁。要是 w₀、b₀ 是确定的,我想计算2025年的年龄,我有一个正确答案和一个通过公式计算的答案,一对比,就知道这个 w₀、b₀ 到底对不对了。
为了进一步讨论,又要开始假设了。假如 w₀ = 1,b₀ = 1,那么 y = x + 1。根据这个函数,我2025年是2026岁,2026 - 18 = 2008,差了2008岁,这明显不对。
看来得做个新假设了。这里有两个变量,我们可以用控制变量法,只调整一个(我在物理学科中学到第一个有用的方法,就是这个方法,记住它,有用极了)。
做一个假设中的假设:假如我开了上帝视角,知道最终这个公式里 b₀ = 1,我只要试遍所有可能的 w₀,代入公式计算,和正确答案对比一下就能找到 w₀ 了。
This, my friend, is called 逻辑。
已知 b₀ = 1,有 y = w₀x + b₀,2025年我18岁,求一个 w₀ 可以让这个公式准确计算我每年的年龄。
- 如果 w₀ = 2,那么 y = 2x + 1,根据这个函数,我2025年是4051岁,4051 - 18 = 4033,这答案更离谱了。
- 如果 w₀ = 3,那么 y = 3x + 1,根据这个函数,我2025年是6076岁,6076 - 18 = 6058,这答案更更离谱了。
生命有限,我没有这么多时间试遍所有数字,让我们用逻辑来加速mental calculation。
通过数学分析可以发现:如果 w₀ = n-1,那么 y(n-1) = (n-1)x + 1;如果 w₀ = n,那么 y(n) = nx + 1,则 y(n) - y(n-1) = x。对于 x = 2025,我发现 w₀ = n 的结果比 w₀ = n-1 的结果大2025。当 n = 1时,计算的结果和18岁的差距已经是2008了,这说明 w₀ 越大,算出的年龄就越大,错得就越来越离谱。所以从一开始假设 w₀ = 1的时候,我们就不应该选择增大的方向。
让我们试试反方向:
如果 w₀ = 0,那么 y = 1,根据这个函数,我2025年1岁,1 - 18 = -17。不管正负,我只关心变化量是17,对比 w₀ = 1的变化量2008,似乎 w₀ = 0更靠谱一点。
但仔细想想,如果 w₀ = 0,那么这个函数就是个常量函数,年龄不会随着年份增加而变化,所以这个结果也不对。
如果继续把 w₀ 减小,根据我们刚才得到的结论,算出的年龄会越来越小,但是这个年龄是负数,所以和18岁差距越来越大。所以这个方向也不对。
根据逻辑推理,w₀ = 1是目前所有可能结果中最合理的,但 w₀ = 1、b₀ = 1对应的函数不对。这说明 b₀ 错了。
寻找正确的b₀
我们可以用类似的方法,给 b₀ 找一个合适的数字。
现在命题变成:已知 w₀ = 1,有 y = x + b₀,2025年我18岁,求一个 b₀ 让这个公式准确计算我每年的年龄。
所以我们可以用类似的方法,给b₀找一个合适的数字。
现在我们的命题变成:已知w₀ = 1, 有y = w₀x + b₀,2025年我18岁,求一个b₀可以让这个公式计算我每年的年龄。
如果b₀ = 2, 那么y = x +2,根据这个函数,我2025年2027岁,2027-18 = 2009,这答案更离谱了。
如果b₀ = 3, 那么y = x + 3,根据这个函数,我2025年2028岁,2028-18 = 2010,这答案更更离谱了。
生命有限,我没有这么多时间试遍所有数字,让我们用来逻辑来加速下mental calculation.
…
如果b₀ = n-1, 那么y(n-1) = x + (n-1),如果b₀ = n, 那么y(n) = x + n,y(n)-y(n-1) = 1, 我发现,b₀ = n的结果比b₀ = n-1的结果大1,n=1时,计算的结果,和18岁的差距已经是2007了,这样说明,b₀越大,算的年龄就越大,错的就越来越离谱,所以从一开始假设b₀ = 1的时候,我们就不应该选这个增大的方向,让b₀增加。
反方向试试。
如果b₀ = 0, 那么y = x,根据这个函数,我2025年2025岁,距离正确的18岁,变化量2007,差距缩小了,更靠谱了一点。
如此类推,最终发现b₀ = -2007,y = x - 2007,这个公式可以准确描述我的年龄随着年份的增长规律。
验证一下:2025年时,y = 2025 - 2007 = 18岁,完全正确!
所以,恭喜我们发现了第一个可用的模型,可以用来预测我的年龄。
知识的传播与概念化
但有个问题:上面的推导过程太啰嗦了,不好传播。我想跟别人讲,并且在这个基础上再做一些假设、产生一些新知识怎么办?总不能每次都完整复述上面的步骤。
一个简单的方式是创造一个词,并且约定这个词等于上面的推导步骤。每次我说这个词的时候,全世界的人都知道我在说这个推导步骤。
但这样不具有通用性,总不能每产生一个新流程、新步骤、新知识就创造一个词吧。
所以,现实世界的第二法则:知识的产生靠归纳总结、造概念、下定义,这样才能更好地传播和进一步深化。
让我们为上述过程建立概念体系:
- 把 y = wx + b 这个描述数据规律的函数,叫做模型
- x叫做特征,w叫做权重,b叫做偏置
- 把通过模型计算的值和实际值之间的差值,叫做损失
- 把 w₀ = 1,2,3,b₀ = 1,2,3 每次计算叫做前向传播
- 在”如果 w₀ = n,那么 y(n) = nx + 1,y(n) - y(n-1) = x”中,把”y(n) - y(n-1)”叫做y关于w₀的变化量。如果w₀变化得足够小,这个变化量就叫做y关于w₀的导数
- 把w₀、b₀改变的方向叫做梯度。上面可以看到,我们希望梯度往下降的方向走,找一个最低点让损失最小,把这个方法叫做梯度下降法
- 每次损失计算后,我们都要反过来调整w₀、b₀,把这个过程叫做反向传播
- 当我们固定b₀讨论w₀的时候,w₀每次都是+1或者-1,其实我们也可以+2、-2,把这个调整幅度叫做学习率。这个步长是我们自己定的,和模型本身没关系,我们管这种参数叫做超参数
定义完这些词后,我们把整个过程叫做”机器学习“。
恭喜,你已经学会了机器学习!
好的,my friend,看到这里,你不知不觉已经学会了机器学习,了解了整个过程。这里面不少词你多多少少都听过,但可能没有真正理解。看到这里,你会发现好简单,人类创造的知识创造也很简单,原来你我都也可以!
当然,这个模型能用的地方很少,只对我和我同龄人有用,其他人就无效了,更不用说其他复杂场景了。
从线性到非线性:模型的进化
所以我们可以继续思考。假设现实中的数据分布像一条弯曲的红色线: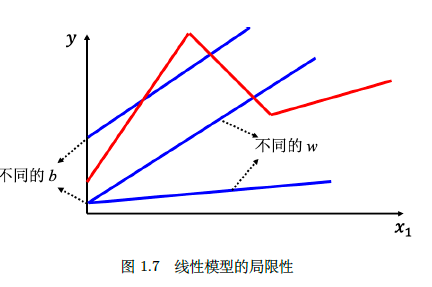
不管w₀和b₀取什么值,线性函数y = wx + b永远也不可能变成像红色弯线一样。聪明的你可能想到可以用多个这样的线性函数叠加,正如圆可以看成无数条线段组成的。
也就是:y = y₁ + y₂ + y₃ + … + yₙ = (w₁x + b₁) + (w₂x + b₂) + (w₃x + b₃) + … + (wₙx + bₙ) = (w₁+w₂+w₃+…+wₙ)x + (b₁+b₂+b₃+…+bₙ)
但这样也不对,==加多少个线性函数叠加起来还是线性函数,不可能像红线那样弯曲==。
圆确实可以看成无数条线段组成,但问题在于线性函数不是线段,而是会不断递增或递减的直线。
激活函数的诞生
要是有一种曲线是这样就好了:中间是线性函数,两边是常量函数。这样就不会一直递增或递减,常量部分可以相互抵消。

这样是有可能的,因为看图: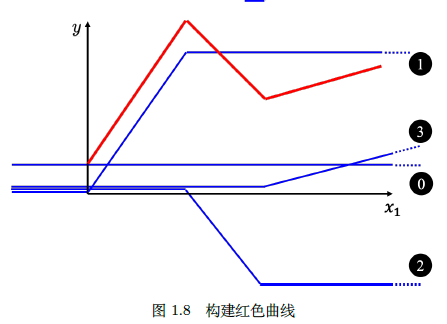
真不幸,这个函数不存在,没办法用一个公式表示,但是数学家找出来了一个函数长这样,并把它叫做Sigmoid 函数,刚才说的更理想的函数叫做 hard sigmoid 函数。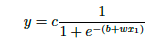
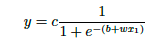
写全sigmoid函数太复杂了,可以用 c·sigmoid(wx+b) 表示这个函数的整体形式。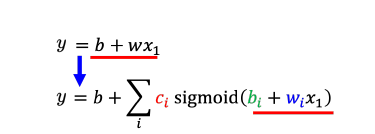
所以从线性模型转化成sigmoid函数,通过组合叠加,得到的新函数可能是任意形状的曲线。这个新函数对应的模型能预测的数据分布就更复杂,也就更有价值。
这个sigmoid函数也叫做激活函数。Oh, human, another word again! 有时候真的很同意灭霸打个响指,让世界随机少一半人。人太多,知识太多,要学的太多了。
从浅层到深度
这个新模型和之前简单的线性模型完全不一样了:
- 有很多特征
- 有多个激活函数的迭代
- 激活函数里的线性函数参数各不相同
- 通过函数得到的y又可以作为输入,再次通过函数计算得到新的y
所以得取个新名字,叫做”深度学习“。为什么叫这个名字?因为取名字的人有话语权。你可能还听过”多层感知机”这个词,其实就是深度学习。感知机就是一层的模型,有了多层后就是多层感知机,如果层数足够多,就是deep了。
深度学习可以这样理解:输出作为新的输入,一次不够来两次,两次不够来三次。这个”很多层”说明层次很复杂,要是纵向看的话,就是很”深度”。
生物神经元的启发
深度学习的全称是”深度学习神经网络”。这个概念是从生物神经元迁移过来的。
生物神经元的解剖结构包括:
- 树突:接收其他神经元的输入信号
- 细胞体:处理信号
- 轴突:传递信号
- 突触:连接其他神经元,通过神经递质释放信号

这看起来和我们刚才讲的机器学习有些类似:
- 特征输入类比树突输入
- 细胞体类比激活函数
- 轴突类比计算过程
- 突触代表一轮的输出作为下一轮的输入
通过这种类比和可视化,我们更容易理解深度学习的工作原理。
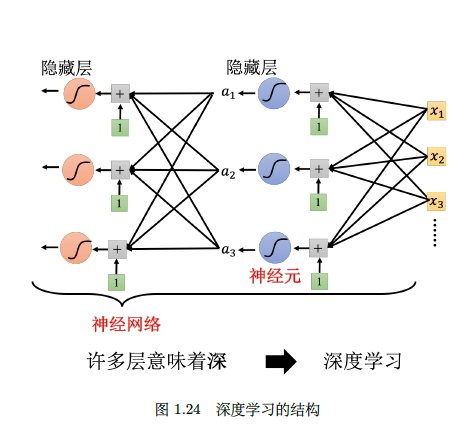
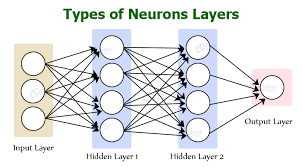
现实世界的第三条法则:可视化,because we are visual animals.
结语
好了,深度学习讲解完毕。
(下面是AI写的)
从一个简单的年龄预测问题开始,我们逐步理解了机器学习的本质:通过数据寻找模式,通过梯度下降优化参数,通过激活函数增加非线性,通过多层结构增加复杂度。
这个过程告诉我们,任何复杂的技术都可以从最基本的原理开始理解。只要我们遵循”从简单到复杂”的逻辑,保持好奇心,每个人都可以掌握看似高深的知识。
现在,当你再听到”深度学习”、”神经网络”、”梯度下降”这些词汇时,你不再是一个局外人,而是一个真正理解其内在逻辑的人。
最后,我对深度学习的理论学习基本上都是从这本书看过来的:《李宏毅深度学习教程》,里面用词比我更专业(虽然意思都一样),我的图片也是里面截取的。